1. Introduction
The algorithm of DeepWalk [1] was first introduced by Bryan Perozzi, Rami Al-Rfou and Steven Skiena from Stony Brook University.
In a word, DeepWalk tries to learn good latent representations, or in Natural Language Processing terminology, embeddings, of vertices in a graph by local information obtained by truncated random walks.
Then how they did it?
2. Motivation
Their motivation actually comes from the wide application of the advanced language models that were first used to extract, unsupervisedly from raw texts, latent distributed representations for words.
2.1. Distributed Representation
To help you better understand what I mean by distributed, let me show you an example.
Prior to the distributed representations, folks normally applied one-hot embeddings to encode words.
For example, suppose there are 6 words in your corpus, “boy”, “girl”, “prince”, “princess”, “king” and “queen”. One-hot representation encodes each word by a vector which has a single one at a predefined location.
| Word | Embedding |
|---|---|
| boy | $(1, 0, 0, 0, 0, 0)$ |
| girl | $(0, 1, 0, 0, 0, 0)$ |
| prince | $(0, 0, 1, 0, 0, 0)$ |
| princess | $(0, 0, 0, 1, 0, 0)$ |
| king | $(0, 0, 0, 0, 1, 0)$ |
| queen | $(0, 0, 0, 0, 0, 1)$ |
Table 1. One-hot representation.
However, these representations do not encode any useful information about the semantics and syntactics of the words.
So, let’s do it in a different way.
Actually, there is no oracle that says the embedding must contain a single nonzero number in a fixed position. So as Yoshua Bengio [2] proposed, why not use a arbitrary vector to represent a word?
Like, why couldn’t “boy” be encoded $(0.12, 3.42, 0.012, 9.18, 14.00, -0.25)$?
Note how it all changes the way we see words computationally. This idea opens up a whole N-dimensional space for us to represent each word. And as you might expect, semantics and syntactics could now manifest themselves as clusters in the space.
But then comes another question – how do we obtain such embeddings?
2.2. Neural Language Model
An explanation of word embeddings is not complete without reference to this paper [3] from Tomas Mikolov. In this paper, researchers proposed an efficient algorithm to learn the embeddings aforementioned. They introduced two independent algorithms, CBOW and SkipGram. But since only SkipGram relates to the work of DeepWalk, I will simply leave the explanation of CBOW to the future.
Formally, SkipGram tries to minimize the negative joint log probability of its context given the embedding of the center word,
\[\text{minimize} -\log(P({v_{i-w} ... v_{i+w}} \mid v_i)),\]where $w$ is half the size of the window that surrounds the center.
By modelling a probabilistic neural language model, or a 2-layer neural network that independently predicts the distribution of surrounding words and minimizing the log-prob, we could learn very powerful and meaningful embeddings.
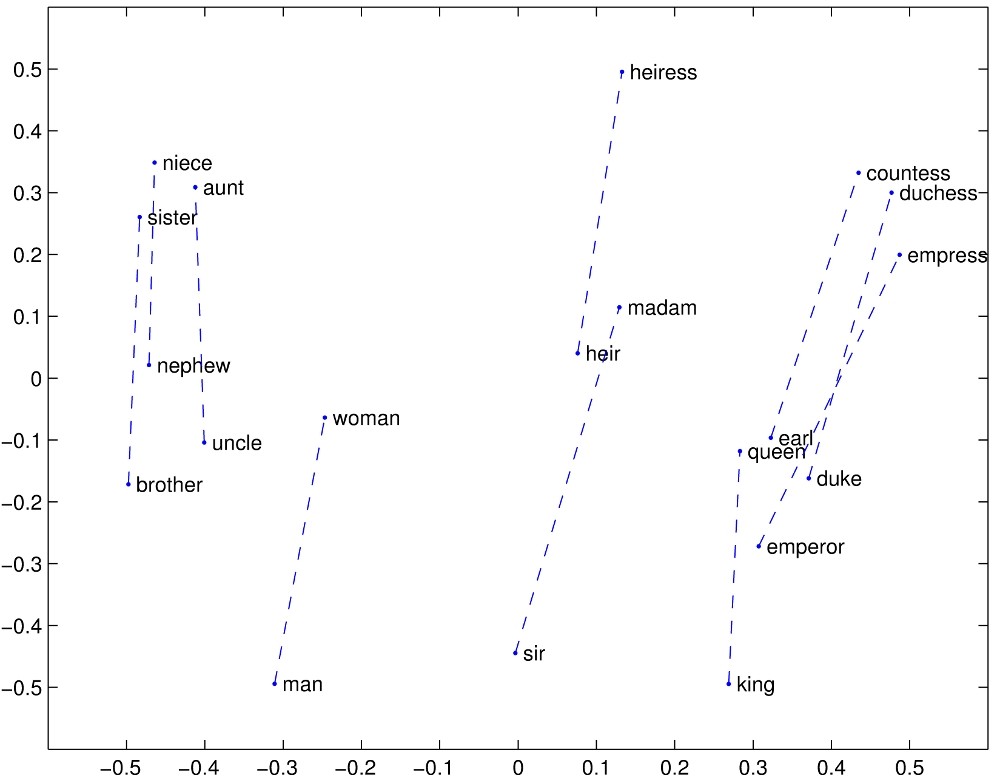 Figure 1. Visualizing word vectors. Notice that words with similar semantics are clustered together.
Figure 1. Visualizing word vectors. Notice that words with similar semantics are clustered together.
2.3. Random Walk
The only essential compartment left to be explained is the concept of random walk. The phrase of random walk is usually encountered in literature of stochastic process. It basically describes a process of transferring randomly among different states or graph nodes.
Suppose you’re in a node $n$ of a graph $G(V, E)$. The node has $m$ neighbors. Then, in a completely random walk, you transfer to any of your neighbor with a probability of $1 \over m$.
Well, I’ve covered all the basics and now let’s move to the algorithm itself.
3. Putting All Together
The algorithm bears the resemblance to Natural Language Processing in that it treats each node as a word in a sequence, which in the algorithm is produced by the random walk, hence the name DeepWalk.
The entire algorithm is illustrated as follows:

In the algorithm, the authors built a binary hierarchical softmax tree to help select words, but since this is only a minor component and the paper has a easy-to-understand writeup for this section, I decide to leave it to the readers to find in the paper.
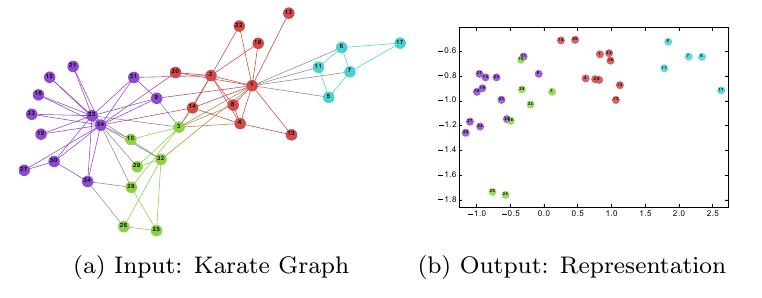 Figure 2. Visualizing DeepWalk. The left plot shows the ground truth while the right demonstrates effective embeddings.
Figure 2. Visualizing DeepWalk. The left plot shows the ground truth while the right demonstrates effective embeddings.
4. DeepWalk Implementation
To help thoroughly understand how the algorithm crunches the data, one should definitely read the source code.
In fact, there have already been a variety of implementations of the algorithm by different deep learning frameworks, including Tensorflow and Keras on GitHub. I would personally suggest the original repository [4] by the authors since it not only retains the source ideas but also shows minimum dependency on other packages. I also have a personal fork [5] that provide a near-complete comments on the formatted source code.
There are several source files in the deepwalk directory.
| File | Function |
|---|---|
| __init__.py | Package info |
| __main__.py | Main algorithm |
| graph.py | Utilities for the graph structure |
| skipgram.py | Wrapper for Word2Vec |
| walks.py | Corpus generation |
Table 2. DeepWalk codebase.
The highest level abstraction is pretty straightforward: generate walks then train.
print("Walking...")
walks = graph.build_deepwalk_corpus(G, num_paths = args.number_walks,
path_length = args.walk_length, alpha = 0,
rand = random.Random(args.seed))
print("Training...")
model = Word2Vec(walks, size = args.representation_size,
window = args.window_size, min_count = 0,
workers = args.workers)
However, details are explained in the corresponding files. If you find it a bit hard to understand the code, feel free to access my fully-commented fork here [5].
5. Conclusion
DeepWalk has made great contribution in the field of network learning and community-based data mining due to its accuracy and scalability.
With the latent representations, people could easily leverage the hidden knowledge in the networks to model similarities among nodes in the graph, making a huge boost in performance for data-related tasks.
If everything goes well, I will update our work on how DeepWalk contributes to knowledge discovery in the near future. So stay tuned!
References
[1] Perozzi, B., Al-Rfou, R., & Skiena, S. (2014, August). Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining (pp. 701-710). ACM.
[2] Bengio, Y., Ducharme, R., Vincent, P., & Jauvin, C. (2003). A neural probabilistic language model. Journal of machine learning research, 3(Feb), 1137-1155.
[3] Mikolov, T., Chen, K., Corrado, G., & Dean, J. (2013). Efficient estimation of word representations in vector space. arXiv preprint arXiv:1301.3781.
[4] GitHub. DeepWalk - Deep Learning for Graphs.
[5] GitHub. Fully-commented DeepWalk.